How to save the world as a mathematician

Suppose your name is Billy Bob and you’re the head of NASA. All of a sudden, one of your employees rushes in and tells you a giant killer asteroid the size of Texas is on its way to Earth, travelling at 22,000 miles per hour¹⁾ and set to collide with Earth in 18 days. Obviously, the first thing you do is tell the scriptwriters they did a bogus job on the science. Someone yells “cut!” and your mind starts to wonder about converting all the units to the metric system.

Take 2. By now we’ve realised we’re in the blockbuster movie Armageddon and no one around seems to have a clue of how orbital mechanics works. So it’s up to us, a couple of brave mathematicians to figure out how to save this planet we call home. Converting the velocity to SI units shows us this thing is travelling at roughly $9.83$ km/s, but it will accelerate towards Earth due to its gravity. The time interval of 18 days tells us that it’s at least $1.5 \cdot 10^7$ km away. That’s about $2.4 \cdot 10^3 R_e$ , which is about ten times closer than the Sun. But wait?! How did we miss this thing? It’s supposed to be the size of Texas!

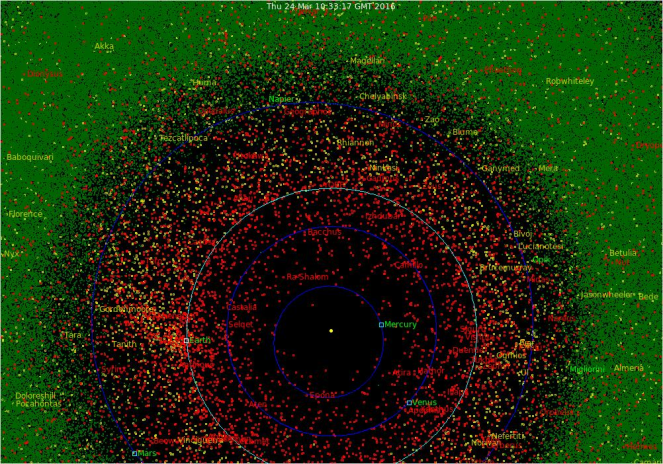
neostorm — Map of the inner Solar system with Near Earth Objects shown. Green dots are objects that do not cross Earth’s orbit and are of the lowest threat level. Yellow dots are objects that do not cross Earth’s orbit but do exhibit a close approach. Red dots are NEOs that cross Earth’s orbit and therefore present the greatest threat. Courtesy of the Armagh Observatory.

Astronomers are actually quite on the lookout for Earth orbit crossing asteroids and comets. Even relatively small ones can cause severe destruction²⁾. I’ve shown here a map of all the currently known potential space hazards. Turns out our neighbourhood is quite crowded. Something the size of Texas would definitely stand out, as it’ll most probably outshine everything but the Moon in the night sky.
Putting that question aside for now, we will first estimate the mass. Texas is about 1244 km by 1270 km, so let’s estimate the asteroid’s diameter as the average of the two, so that we end up with a ball of 629 km radius. Rock has a density of roughly 2.5 (metric) tons per cubic meter, giving an estimated mass of $2.6 \cdot 10^{21}$ kg, or about $4.4 \cdot 10^{-4}$ Earth masses ( $M_e$ ). It turns out our mystery object is actually Charon, one of the moons of Pluto, which is roughly this size and mass³⁾.

Charon,_Earth_&_Moon_size_comparison — Earth, the Moon and Charon (a.k.a. the killer asteroid) size comparison.

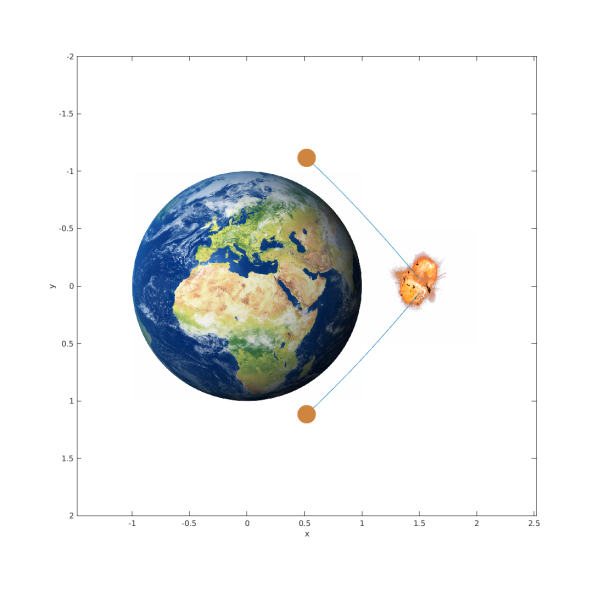
Now that we know some more about this killer asteroid, let’s try the solution that the “scientists” in the movie tried: blow it up at absolutely the last possible moment. Luckily for our fictional friends, the asteroid breaks into two perfect halves while the nuclear explosion drives both pieces exactly far enough away from the Earth. One excited NASA employee exclaims that “it’s going to miss by 400 miles!”, which is about 650 km. Although that’s technically far enough for the Earth to survive, if the centre of mass of each half passes this close, both parts will plough straight through the bottom layers of the atmosphere. In fact, passing this close, they might just knock over a few buildings and tear up the surface by their gravity. And that’s just if they don’t explode due to the immense heating by the atmosphere.

The setup

Having estimated the mass, velocity and position relative to Earth, we can construct our simulation. As you might have guessed, this is done by something called Hamiltonian dynamics. It involves finding the total energy of the system and deriving from it a set of ordinary differential equations that govern the motions.
For simplicity’s sake, let’s set $t=0$ at the time right after the nuclear bomb went off, so that we’re dealing with two equally large chunks of $m = 2.2 \cdot 10^{-4} M_e$ that start out in roughly the same position. The Hamiltonian $H$ for this system, for $t>0$ , can be found by adding up the orbital energy of both chunks plus the interaction potential,

$H =\frac{\| \mathbf{v}_1 \|^2 }{2} + \frac{ \|\mathbf{v}_2 \|^2}{2} - 32 \pi^2 \left( \frac{1}{r_1} + \frac{1}{r_2} + \frac{\alpha}{ \| \mathbf{x}_1 - \mathbf{x}_2 \| } \right)$

Here, velocity is indicated with $\mathbf{v}_i$ with $i = 1,2$ representing the chunks. The positions are indicated with $\mathbf{x}_i$ with Earth being in the origin of our coordinate frame, with distances are indicated as $r_i$ . The number $\alpha$ is the mass ratio of the chunks and the Earth, with a numerical value of $2.2 \cdot 10^{-4}$ . The equations have been scaled in special units of distance and time so that we may conveniently express everything. The distance has been scaled with Earth radii while time has been scaled with the time it would take a satellite to orbit the Earth at one Earth radius above the surface, which is roughly 4 hours.
Using Hamiltonian dynamics, the time evolution of the system, relative to Earth, can be expressed with Hamilton’s equations,

$\dot{\mathbf{x}}_i = \frac{\partial H}{\partial \mathbf{v}_i }$ ,
$\dot{\mathbf{v}}_i = -\frac{\partial H}{\partial \mathbf{x}_i }$ ,

where choosing $i$ equal to 1 or 2 picks which chunk. We start our integration with a single asteroid some 2400 Earth radii away with an initial velocity of $22.0$ in our units⁴⁾. At position $x_0$ blow up the asteroid into two chunks by giving one a positive velocity in the $y$ -direction, $v_0$ , and the other one $-v_0$ . For each position $x_0$ , we’ll gradually increase $v_0$ until the two chunks miss Earth by the magic 400 miles. We’ll account for the finite size and we’ll take a bit of extra margin, so that the chunks actually miss the lower atmosphere by 400 miles. Hence, we’ll call it a miss if the centres of mass miss by more than 0.16 Earth radii.

Maximum effort

Before I show the results, I would like to briefly discuss the unit of energy I’ve used to express the strength of the bomb. Ordinarily, the unit of choice when it comes to blowy-uppy things is TNT equivalent, that is to say how much TNT would be necessary to achieve the same bang. For instance, the Little Boy atomic bomb dropped on Hiroshima was worth about 15 kilotons of TNT. However, as a unit of energy I’ve used the energy released by the most powerful nuclear bomb ever detonated. This bomb is known as the Tsar Bomba, worth about 50 megatons of TNT, although it could theoretically be pushed to 100 megatons. For arguments sake let’s just use the 50 megatons of TNT equivalent to work with.
The Tsar itself is quite heavy, about 27 metric tons, which means we could in theory launch one bomb towards the asteroid on top of a Saturn V booster. The Saturn V launched the Apollo astronauts to the Moon and remains, to this day, the most powerful booster every brought to operational status. We can therefore launch the most powerful every on top of the most powerful rocket ever at the asteroid. Hence, one unit of energy represents Humanity’s maximum effort.

The movie events

The events depicted in the movie Armageddon show how the bomb is detonated at the very last possible moment. The “zero barrier” actually seems to be within an Earth radius, at about half an Earth radius away from the surface, so let’s start with detonating there.

frame10 — Simulation result in the movie situation. The explosion required 1.63 TeraTsars.

At this extremely close distance to the Earth, the explosion would need $1.63 \cdot 10^{12}$ Tsars, that is 1.63 TeraTsars, more than a million million times the current human capability. We all know that movies tend to take some artistic freedom when it comes to physics and reality, but this one takes the cake!

How about not at the last moment?

At this point, the mathematician trying to save the world would scratch his head and will conclude that the movie option seems to be a bad one. Perhaps there’s better choices for how far away we should detonate to use the least amount of bang to save our bucks.
So let’s start with relatively short distances, from the extreme case of the movie to a hundred Earth radii out, which is roughly twice the distance of the moon away.

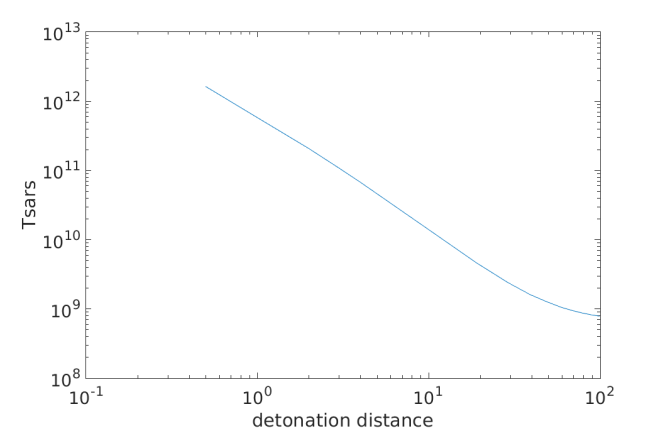
short_distance — Loglog plot of the minimum number of Tsar bombs necessary to avoid asteroid collision versus distance from the surface in Earth radii.

The graph shows a loglog plot of the energy required versus the distance, which means both distance and energy are on a logarithmic scale. This type of plot is particularly useful when both quantities vary over a large range. From the figure, we can see that detonating further out from Earth, we’ll need less bombs. In fact, if we detonate at a hundred Earth radii instead of half an Earth radius above the surface, we’ll actually need a thousand times fewer bombs. Although that’s still nowhere near what we are capable of, it’s pretty great! This effect is known as sensitive dependence on initial conditions. Tiny changes can have large effects over long times. So let’s see what happens if we detonate even further away. This time, I’ve plotted the result in a regular (linear) plot.

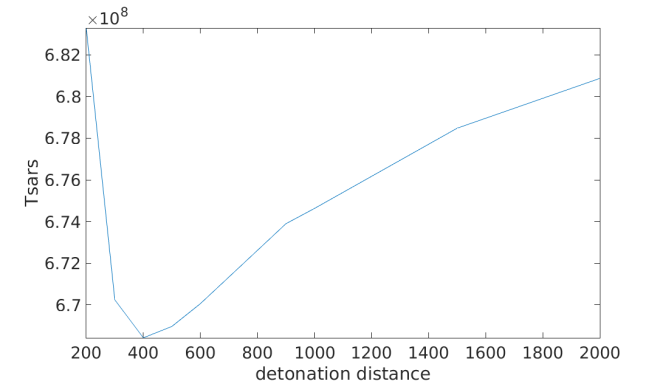
long_distance — Minimum number of Tsars to avoid collision versus the detonation distance in Earth radii.

This time, I’ve plotted the data on a linear scale. The detonation distance varies between 200 and 2000 Earth radii. The largest distance is roughly where the asteroid is discovered in the movie. Something immediately springs to the eye, there is a minimum energy requirement at 400 Earth radii out. However, even at this optimal detonation distance, we still need 670 MegaTsars, or 670 million Tsar bombs. Further away and we need to increase the energy again to save our home planet. What’s happening here is that the asteroid chunks are attracting each other and the asteroid is recombining.
Indeed, if we were to travel along with the asteroid while the bomb blows up, no momentum is imparted to the asteroid as a whole. Given enough time, the mutual gravity of the asteroid chunks can pull the asteroid together again. If we blow up the asteroid further away than 400 Earth radii, we’re not so much trying to overcome the Earth’s gravity as the mutual gravity of the asteroid itself. This principle is ultimately why trying to blow up an asteroid is always a poor idea regardless of the size.

What should we do then?

If Charon is on its way to Earth, trying to blow it up is certainly not going to help. Given enough time, it is very likely that such an asteroid will reassemble by the mutual gravity of its parts. In the end, it has to do with momentum transfer, or the lack thereof. Trying to blow up an asteroid will result in zero momentum being imparted to it in total. So that’s the trick then, instead of blowing it up, we need to nudge the asteroid out of the way, off its collision course. We may send a rocket up there that pushes it a little bit over an extended period of time. But what if the asteroid is spinning, or if it’s made of a bunch of small rocks held together by their mutual gravity.
The best idea seems to be the gravity tractor, where a spacecraft hovers close to the asteroid, letting gravity do the work. We’ll need to do it years in advance, since the total momentum transfer would be tiny, but here sensitive dependence on initial conditions comes to the rescue. By intervening a long time in advance, a tiny change is going to have very large effects and a small gravity tug can indeed pull a large asteroid off a collision course.
In the end, it seems that even though Armageddon takes some staggering artistic liberties when it comes to physics. It’s a rare and beautiful thing when we can actually quantify exactly how wrong movie physics are. However, Armageddon does teach us the importance of early warning systems for avoiding asteroid collisions. In the movie, the asteroid is discovered way to late to do anything about it, but if we know years in advance which asteroids might potentially hit us, we have a shot to save Earth.

1) Yes, imperial units. *sigh*

2) The asteroid that caused the dinosaur extinction is estimated to have a radius of around 10 km.

3) New Horizons recently took some nice pictures of it. Guess what? It’s round. Objects this massive usually are, the gravity tends to contract it into roughly spherical shape.

4) By sheer coincidence, it turns out that our unit of velocity is very close to 1000 miles per hour.

Bart's Blog